The task of building distributed application network is plagued by cost, ambiguous requirements and schedule overrun. A fundamental problem in building distributed applications is the presence of unreliable estimation to formulate the list of requirements in the initial stage of project life cycle. Subsequently, this often leads to reactive response from decision-makers against error occurrences, leaving a very small space for developers to establish forward planning. Unless estimations are enhanced to include more sophisticated verification and validation methodologies, the problem will remain. This paper looks at Petri Nets as a modelling and simulation instrument to verify and validate models of distributed application networks.
1. INTRODUCTION
Historically, life critical software projects have routinely incurred significant checks, simulation and validation in order to reinforce the safety protocols and this approach does now apply also to critical business applications. In attempting to incorporate the simulation strategies in business critical systems, researchers in software engineering have developed several simulation tools with the intention of improving the effectiveness of estimation. An emerging area of research takes into account methodologies such as formal methods. Languages like B- method, pi-calculus and the Z notation [2] provide mathematical formalism to illustrate and evaluate consistencies in software projects.
Building distributed multi-component systems introduces another layer of uncertainty, which very much depends on the underlying network and infrastructure. In this paper we particularly concerned with mobile communication and its infrastructure. The wireless networks with their mobile clients differ from traditional client server models and given that numerous wireless devices are likely to increase [1], the process of integrating those devices under a single server solution can become very complex and inefficient as the network grows. A more practical solution is to operate these mobile devices over a decentralised distributed application system [15]. In this work, the research questions the requirements that exist in building a highly distributed network applications and investigates if simulation can be resourcefully established to examine the model of a particular network. The work focuses on modelling communication agents based on the blueprint of the Virtual Mobile Redirector (VMR) [4] queue structure and subjects it to Petri Nets [3] simulation to carry out a number of experiments. The experiments include several simulation scenarios which when combined together yield an estimation of the agent’s performance and simulating different agents operating in tandem provides a fairly accurate approximation of the network performance.
The paper starts with a brief description of Virtual Mobile Redirector together with the problem domain, and Quality of Service (QOS) issues in a networking environment. Then, the simulation and modelling environment is presented. This is followed by describing the simulation process together with a number of experiments. Finally, we conclude with some suggestions for future work.
The Virtual Mobile Redirector (VMR) is a multi agent messaging system which enables mobile phones to connect to IP based application through protocol conversion [4]. The application consists of different interconnected software agents, wherein an agent encapsulates a series of methods as one class function and comprises of input/output components expressed as “sensors” with the primary purpose to receiving and dispatching packets of information via queues (sensor class). The agent also contains a processing unit, which identifies which methods are to be triggered when the sensors receive data.
The VMR represents a logical organisation of agents, which interact in a common environment to achieve a particular goal. It focuses on the collaborative resolution of global problem by a set of distributed entities. Like typical Multi Agent System (MAS), the VMR abstracts the interaction between individual agents, defining the independency of the underlying architecture, which can be deployed on both centralised and highly distributed systems. The VMR agents communicate using interconnected queues which are typically the most commonly used data structures within the implementation of communication mediums (substratum) for distributed systems [14]. Queuing theory is the mathematical study of queues within a system which is essentially applied to analyse attributes such as performance, robustness and reliability of multi programmed computer systems.
The VMR architecture has been established on a hierarchical structure of a Multi Agent System (MAS) which can be decomposed into three levels of controls; 1) the agent level, 2) cluster level and 3) system level. Each level has different structures, activities and mechanisms, but the levels interact with each other during local / global communication. The fact that the VMR was designed in a symmetrical and hierarchical manner, it enabled us to design the simulation of the model based on the hierarchical features of Coloured Petri Nets, though the process is not a one to one mapping, it still helped in the design translation process as will be discussed in the following sections.
Simulation aims at observing a system enforced to react under a number of predefined circumstances to finally evaluate the behavioural outcome [6]. A key factor, however, prior to simulation, is to underline what features of the system one needs to simulate in order to maximise knowledge capture with a minimum amount of resources. Considering a distributed application network, at the highest level of observation, the features that a simulator should question are distinguished by five entities [7]. First, for a given network architecture, the task requires knowing the amount of data entering and leaving the system. This is termed as the traffic rate. For example, a network designer is required to decide on the size of a queue component over a network against the traffic rate.
Second, the traffic inside the network may be congested and the designer would be required to know the congestion rate so as to alter the specification of the network for better performance. Third, the rate at which the data is flowing inside the network is also crucial to identify the latency that through simulation can be calibrated to an acceptable level. Fourth, is the throughput; the designer will need to know the delivery rate of the network under different condition. Throughput is usually the first measure that the customer investigates [1]. Finally, data loss is yet another important factor that illustrates how reliable the network system is. The above five entities form the programme’s framework and are termed as the Quality of Service [7] [13].
The Quality of Service of a network is described by its performance, i.e. how efficiently the system delivers its service to the world. Hence, acquiring knowledge on the quality of a system prior to product deployment would be competitive gain for any organisation building network application. We propose that to measure the Quality of Service of a distributed network application at the early stage of development imply the use of simulation tools since a real network system is not available at that level. This can be done using the five entities described earlier; the simulation engine should derive test scenarios to observe the network behaviour and reaction when any of the entities is questioned. The outcome from the simulation is analysed to develop contingencies and self-protecting mechanism when and where required [5]. In this paper we refer to these contingencies as handlers [7]. Each of the entities has their handlers. We hypothesise that a successful simulation procedure should be able to search and locate deficiencies related to the any of the five entities and next propose, with an acceptable degree of error, the appropriate handlers for recovery. The simulation can then test out such a procedure using four different measures to handle the five entities:
(i) Traffic metering to control and monitor traffic rate.
(ii) Resource allocation strategy to boost resource performance should the rate of throughput falls.
(iii) Data drop policy to regulate the rate of data loss.
(iv) Switching / Routing (Re-routing) strategy to alleviate congestion rate over the network.
(v) Resource allocation strategy to reduce network latency.
To evaluate the quality of service of a distributed network application, the experiments should look at three features of performance; namely the entities traffic rate, throughput and latency. The simulation scenarios position the Petri Net model of the network application under different situations whilst the experiments distinctively track the network behaviour and relate the relevant handlers for each situation.
In the last three decades research in computer science strongly contributed to the generation of simulation tools. Several formalisms and related automatic tools have been developed, others extended to accommodate simulation engines and are currently available on the market. Within the wide spectrum of simulation techniques, we were required to focuses on a selected subset of simulation tools [8–11], which represents, either for historical reasons or recently achieved popularity, and subsequently choose a platform that best agrees with the basic entities needed to model and simulate a distributed network application, which is Petri Nets in our case.
Petri Nets are a formal modelling technique for the description of concurrent and distributed system behaviour [3]. Since their introduction in the 1960s they have impressively evolved. Currently, several versions of this graphical modelling language exist, which find widespread application in specification, verification, and performance analysis of distributed parallel systems, communication protocols included. Typical applications of Petri Net are in the field of communication protocols, telecommunication networks, and software engineering. Despite a modelling philosophy that is not easy to be acquired,
Petri Nets, with their engaging graphical notation are a powerful modelling language to describe and investigate communicating and resource-sharing processes. Coloured Petri Net combines the basic formalism with programming language CPN ML [3] to enable the creation of accurate system models taking into account temporal and stochastic issues. Similar to other graphical tools, embedding user-defined functions into the specification is an interesting possibility to avoid heavy graphical descriptions of deterministic calculations. For undertaking the experiments, we considered CPN Tools, a freeware Coloured Petri Net tool available on the market. CPN Tools is a new platform for modelling and simulation of Petri Nets, which allows editing, simulating and analysing Coloured Petri Nets (CPN).
The models as well as the procedures of the experiments are discussed in this section. The aim is to carry out an investigation as to how Petri Nets are utilised to simulate the VMR multi agent system (VMR MAS) at the highest level and the communication agent queue component at the lowest one. Thus, the information from the exercise can be statistically interpreted so that handlers (contingencies) can be formulated for the necessary QoS measures.
5.1. Modelling and Simulation
When making use of the hierarchical decomposition feature of CPN, we are able to describe the architecture of an agent-distributed system at different level of perceptions. At the highest level of expression, we modelled the incoming of data packets from the external networks to the VMR system which is illustrated in Figure 1.

The CPN model starts with the transition Dispatch receiving one packet at a random time, which follows a Poisson distribution with a mean of 5.0 ms, from an external source. Since the model is a timed Petri Net, variable E at place M is timed in millisecond whilst each packet is numbered at the place TICKER, thus the place Dispatch (P1), knows about the packet number (packetNo). Next, at transition Dispatch, a function ch() is triggered to randomly select between 2 transition operations, either Translate Packet or Decrypt Packet. These functions add more knowledge to the model; hence during simulations more complex processes can be investigated in an attempt to mimic reality as closely as possible. Inside the transitions Translate Packets and Decrypt Packets, there are a series of distinct software agents communicating to each other with a common objective. In the VMR system, operations like “translate the packet structure to a general format” are performed by a cluster of agents. In an attempt to simulate these functions, we constructed a hierarchical transition Translate Packet within which are a group of agents connected to each other, and the same design applies to the transition Decrypt Packet.
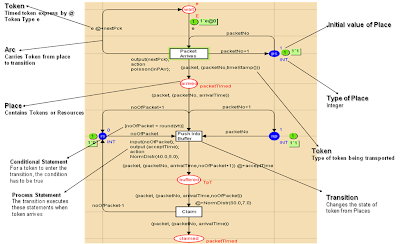
Figure 2, depicts the internal design of the transition Translate Packet, wherein, several agents are non-linearly assembled. Packets move concurrently across the agent system which is supported by the CPN infrastructure for such dynamic data movements. An agent receives the packetNo and the arrivalTime from the place DISPATCHED. As the packet travels from one agent to another, the task of translating a message to a generic format is distributed among various agents. Drilling further through the Petri Net hierarchy, we find the design of one agent which triggers several processes towards translating a packet into different formats. However, for simplicity we only present a model of the lowest level of the hierarchy, the FIFO queue sub-net structure (Figure 3), that buffers all the packets that reaches the agent, and which represents the communication medium of each agent, found in the sensor class of the VMR (see section 2). The queue component resides within the sensor class of an agent with the value vh, being dynamic and adjustable during simulation, indicating the top stop mark capacity of the queue’s buffer and when hit, it blocks the packet entry. Unless the buffer is freed, outgoing packets have to wait for their acceptance. Another watermark is the high watermark denoted by h, and when reached, the rate of incoming packet is decreased until the number of packets inside the queue’s buffer reaches the low water mark which indicates that the queue is within normal parameters of operation and no protective measures are required.
When the Transition Packet Arrives is fired, the queue receives a new packet, hence a token is added to the place arrived. Upon arrival, each packet is paired with a number, (see place packet stamped), which contains a time stamp and it is equal to the current model time, created by means of the function timeStamp(), on the arc between Packet Arrives and arrived. The place arrived characterises the packets that reached the queue and are waiting for clearance. Next, the queue pushes the packet into its buffer and the waiting line is shown by the occurrence of the transition PushIntoBuffer.

The arcs between NextPacket and PushIntoBuffer ensure that packets are loaded into the queue in the same order in which they joined which enforces the FIFO structure. When packets are loaded onto the buffer, shown by the place buffered, they are counted (see the inscriptions on the arcs between PushIntoBuffer and buffered, noOfPackets). At this point, packets are inside the buffer and waiting for the next run where the queue might perform some simple processing to the packets before releasing them. Once one packet completes its processing cycle, a token is added to the place leaves. Any claims from the place, causes the transition Claims Packets to be fired which finally state that a packet has left the queue.
The model is an integer-timed Petri Nets, i.e. the queue is processed with relation to time. The Poisson function, at the entry point is used to model the inter-arrival time for packets, and it can be found in the code segment associated with Packet Arrives. By changing the value in the function’s argument, the mean of the Poisson is altered and thus providing different spectrum of simulation conditions. The function CalcAccTime() in the code segment for the transition PushIntoBuffer to calculate how much time is needed for loading a given packet. The function NormDistr() is used to calculate how much time is used for a packet to be processed, as shown in the code segment for Process. This is particularly useful when one needs to make a number of simulations using different parameters.
In summary the objectives of the simulation of the VMR CPN model are as follows:
(i) To observe the percentage time a unit (packet) leaves an agent given a high input rate. This is to probe the information on the throughput of the queue during high input to the VMR system.
(ii) To observe the average time a unit (packet) spends in the VMR System. This is to provide information on the likelihood of out-of-time packet(s), should the latter wait excessively in any queue buffer of any agent.
5.2. Results and Observations
The simulation exercises investigate how packets move amongst the VMR Agents, with variable parameters at different level of hierarchy. The model was fed with packets at random intervals and the output was observed and recorded. The experiments were broken down into two series (experiment 1 & 2).
• Experiment 1 explains that the queues inside the agents resorted to protect themselves whenever the time interval between incoming packets was smaller than the service time of the queue, which consequently resulted in some packets being rejected.
• Experiment 2 stresses on the likelihood of out-of-time packet in the VMR System. This is defined by a function of the agent’s internal latency, queue’s buffer size and the input rate at the receiving end. It confirms that while attempting to gracefully slow down the number of packets entering the buffer, should an overflow occur; the queue inside an agent consequently causes packets to wait longer in its buffer.
Experiment 1 starts by investigating the percentage unit time (ms) a packet leaves the multi agent system given a burst of input. The objective is to observe the throughput of the system in unconditional circumstances and evaluate its behaviour and efficiency to protect itself. We run through three simulations of 4000 steps and at step 1000 , we changed the Poisson mean from 1 packet per 10 ms to 1 packet per 3 ms, which provided the scenario for the burst and is the type of situation common to the domain of messaging. At each simulation we decreased the value of the watermarks, thus decreasing the waiting line in view of achieving conditions where packets have to wait longer to be serviced.
 Figure 4 runs through the simulation as the buffer sizes of the queues inside the agents were increased. We sampled the data into batches of 100 ms interval and recorded the number of packets entering and leaving the queue. Given a burst in packet entry, the graph shows the difference between the input rate and the output rate. The close proximity between the input and output rate justifies that that the service rate of queues within the VMR system is adequately lower than the input rate given an input rate of 100 packets per second (1 pck/10 ms) and a burst of approximately 350 packets per second (1 pck/3 ms). The simulation validates both decisions on the buffer size of lower limit 10 and upper limit 20.
Figure 4 runs through the simulation as the buffer sizes of the queues inside the agents were increased. We sampled the data into batches of 100 ms interval and recorded the number of packets entering and leaving the queue. Given a burst in packet entry, the graph shows the difference between the input rate and the output rate. The close proximity between the input and output rate justifies that that the service rate of queues within the VMR system is adequately lower than the input rate given an input rate of 100 packets per second (1 pck/10 ms) and a burst of approximately 350 packets per second (1 pck/3 ms). The simulation validates both decisions on the buffer size of lower limit 10 and upper limit 20.In experiment 2 we investigate the period of time a packet stays in the VMR at a given queue of an agent and draws the distribution of the packet’s lifetime. The experiment reports on the time taken for a large sample of packets to leave any queue of an agent. The objective was to estimate the number of out-of-time packet that exists given an input burst and a decrease in the buffer size. We analysed the period of time a packet takes to leave an agent, e.g. over hundred packets take 12 ms to leave the queue of a VMR agent. Hence using such analysis, a threshold can be established to identify the packets that have a probability of being out-of-time when claimed. For instance, should the out-of-time threshold be marked at 15 ms, any packet beyond this mark is irrelevant for the system.
The experiments show how Petri Nets can be exploited to mine appropriate data so that the potential behaviour of a model under a set of parameters can be known. The obtained results provide a very good idea about the performance of the model, hence the formulation of directives prior to product deployment. If we look back at experiment 1 where a discussion on burst of input rate is presented, this is often very true in the mobile telecommunication and messaging systems. For instance, if we consider the message entry to a SMS Centre (SMSC) for one day, there is a pattern, wherein bursts can be found during the morning when people wake up and starts sending text message and burst at lunch time during their break time. To deal with the surge, system designers over-estimate the buffer size of queues within their systems, which is very inefficient in terms of resource allocation and economic viability. However, using simulation based on historical data of typical message distribution, one can provide a range, a lower limit specification size for off peak period and upper limit specification size for peak period. This is type of design is called design for capacity, which is a competitive advantage if possessed. Moreover, the simulation of the VMR model can be used to capture the user requirements at the early stage of the life cycle. This can be done by translating these requirements into the Petri Net simulation model which can help in identifying and observing the different behavioural patterns under different requirements. For example, if the user requirements place an important weight on reliability aspects of QoS, implying the high priority of reducing data loss, resources can be allocated within the model to reflect the importance of this requirement. Moreover, the simulation will provide detailed observations on the impact of increased reliability on other QoS parameters, particularly performance, as well as its impact on resource allocations i.e. cost. Thus, such observations provide more knowledge to enforce better accuracy for quality estimations, in terms of QoS.
6. CONCLUSIONS
The paper presented an approach for modelling and simulation a multi-agent messaging system (VMR) using multi-level Petri Net formalism and CPN Tools. The paper also presented the potential of capturing and estimating the user requirements at the early stage of the software life cycle. As it can be observed, Petri Net is an adaptable tool, i.e. it allows alterations to a model so as to retrieve the necessary information from it. Two experiments were conducted to show how simulation can be executed to question a model. The results and observations provided more knowledge to enforce better accuracy to estimations particularly at the early stages. In terms of QoS, it shows how Petri Nets can be exploited to mine appropriate data so that the potential behaviour of a model under a set of parameters can be known. The obtained results provide a good idea about the performance of the model prior to product deployment.
REFERENCES
1. Price Water House Cooper, “Technology Forecast: 2009”, 2009.
2. J. M. Wing, “A Specifier’s Introduction to Formal Methods”, IEEE Computer, vol. 23, 1990.
3. Kurt Jensen, “Coloured Petri Net – Basic Concepts, Analysis Methods and Practical Use ”, Vol 1, 2nd Edition, Springer, 1997.
4. Empower Interactive Group Ltd, “Virtual Mobile Redirector Manual Guide”, 2003.
5. Roger S. Pressman, “Software Engineering, A Practitoner’s Approach”, 5th Edition, McGrawHill, 2000.
6. Cisco Systems, “IP Quality of Service, – The complete resource for understanding and deploying IP quality of service for cisco networks”, Cisco Press, 2004.
7. J. Ellsberger, D. Hogrefe, and A. Sarma, SDL Formal Object Oriented Language for Communication Systems, Prentice Hall, 1997.
8. C-M. Huang and J-M. Hsu, “An Estelle-Based Probabilistic Partial Timed Protocol Verification System,” Int’l. Conf. Parallel and Distributed Systems, 2004.
9. T. Bolognesi and E. Brinskma, “Introduction to the ISO Specification Language LOTOS,” Computer Networks and ISDN Systems, vol. 14, Apr. 1987.
10. L. Millett and T. Teitelbaum, “Slicing Promela and Its Applications to Protocol Understanding and Analysis,” Proc. 4th SPIN Wksp., Paris, France, 1998.
11. Nam, S.Y., Sung, D.K., “Measurement Based Delay Performance Estimation in ATM Networks”, Globecom, 2000, pp. 1766–70.
12. Mouharam, A.A.K., “Monitoring Quality of Service on Broadband Networks”, PhD Thesis, Kingston University, 2002.
13. Makoond, B, “An Integrated Modelling Framework for the Design and Constructions of Distributed Messaging Systems”, PhD Thesis, Kingston University, 2008.
14. Khaddaj S, B Makoond and R Oudrhiri, “Distributed Computing Techniques for Wireless Messaging Systems” in ‘Journal of Algorithms and Computational Technology’, Multi-Science Publishing Co Ltd, 2008, pp. 1748–3018. Journal of Algorithms & Computational Technology Vol. 4 No. 3 323